Question
A rugby player passes the ball 7.00 m across the field, where it is caught at the same height as it left his hand. (a) At what angle was the ball thrown if its initial speed was 12.0 m/ s, assuming that the smaller of the two possible angles was used? (b) What other angle gives the same range, and why would it not be used? (c) How long did this pass take?
Question by OpenStax is licensed under CC BY 4.0
Final Answer
  1. 14.2∘14.2^\circ
  2. 75.8∘75.8^\circ
  3. 0.60 s0.60 \textrm{ s}

Solution video

OpenStax College Physics, Chapter 3, Problem 30 (Problems & Exercises)

OpenStax College Physics, Chapter 3, Problem 30 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 3, Problem 30 (PE) calculator screenshot 1
  • OpenStax College Physics, Chapter 3, Problem 30 (PE) calculator screenshot 2
Video Transcript
This is College Physics Answers with Shaun Dychko. A rugby player is throwing a ball at 12 metes per second and at some angle theta that we have to find above the horizontal. And the ball goes seven meters to the receiver here and that's a horizontal displacement or also known as the range of this projectile. So if it returns to the same height as it was thrown, then this range is given by this formula here, which is equation number 71 in chapter three; It’s the initial speed squared, times sine of two times this launch angle, divided by the acceleration of gravity. So we can solve for theta eventually by first of all multiplying both sides by g over v naught squared. Then switch the sides around and we would have sine two theta is R times g, over v naught squared. And then take the inverse sine of both sides. So on the left we have 2 theta and on the right we have inverse sine of the range, times acceleration due to gravity, divided by initial speed squared. And then divide both sides by two and now we have theta. So it’s the inverse sine of Rg over v naught squared and then that answer to the inverse sine is then divided by two. So inverse sine of seven meters, times 9.8 meters per second squared, over 12 meters per second squared. All divided by two. And that gives 14.2 degrees. Now, there is another answer for this question as to what this angle would be. Such that a 12 meter per second ball would have a range of seven meters. And that's an answer which has a much larger angle. And a quarterback would never throw at the larger angle, because doing so would create a longer duration of flight. It would take a longer amount of time for the ball to travel and that time gives defenders a chance to get in the way. So they always try to aim for the lower angle that will achieve the same range. Okay, but in part B just for fun, we're going to figure out what that other angle would have been. So, I guess we can start with this up here. We can say, sine two theta is Rg over v naught squared. This Rg over v naught squared, if you plug it in; seven meters times 9.8 divided by 12 squared, it's about .4 or so. nd that is the y-coordinate of a point on this unit circle. And the unit circle has a radius of one. And if this picture is not familiar then my explanation here might not make that much sense. But hopefully you've seen this picture before. So, yes, when you figure out the inverse sine of the number. What you're given is the reference angle. And so that's the angle here between the positive x-axis and the terminal arm, that is in this first quadrant. But there's another angle which also has the same sine because it has the same y-coordinate. And the y-coordinate of these two points are the same and y-coordinate is the sine of whatever this thing is here. So that means there are two angles which give the same sine. And so in this question we're going to figure out what the second angle is. So when you take the inverse sign of Rg over v naught squared, you're finding two times theta. Because that's the argument for sine here, and that is 28.4 degrees. And so the second answer is going to be the full straight line angle, 180 minus the 28.4 degrees. Because this terminal arm here will have the same reference angle. That is the same wedge between the terminal arm and the x-axis. So 180 minus 20.4 is 151.6 and dividing that by two gives a second angle, 75.8 degrees. Okay, part C says, how long did the ball spend in the air? Well, we know that the final x-position is going to be the initial x-position plus its initial x-velocity times time, plus one half times acceleration in the x-direction, times time squared. Well there is no acceleration in the x-direction. And will define the initial position at the quarterback to be zero. In which case the final position then is just this x-component of the velocity, multiplied by time. And this x-component is the adjacent leg of this right triangle here, where we have this being the vertical component and this being the x-component here. And we use cosine of this angle theta multiply by the hypotenuse of 12 meters per second to figure out the x-component of the velocity. So we can solve for t by dividing both sides by v naught cos theta and then switch the sides around and we have time then that is the final position divided by initial speed, times cos of the angle. So that’s seven meters, divided by 12 meters per second, times cos of 14.2 degrees which is 0.60 seconds.

Comments

Why is gravity a positive value? I see in the end result, it should be a positive value or else we have a negative angle, but how are we supposed to know when we consider gravity a negative or positive value?

Hi georgeh, thanks for the question. The variable gg is meant to always be positive. It's the magnitude of the acceleration due to gravity. In some questions, sure enough, 'gravity' is negative, but that's represented by a negative sign explicitly in front of gg. When using one of the regular kinematics equations where you have a factor aa, where aa is the 'acceleration due to gravity, this would get replaced by −g-g (assuming you're working with a coordinate system where down is negative). I can totally see how this gets confusing, since gg is also commonly named 'the acceleration due to gravity'! The full, proper name for gg should be the magnitude of the acceleration due to gravity, but that's too wordy, so it's call 'acceleration due to gravity' for short.

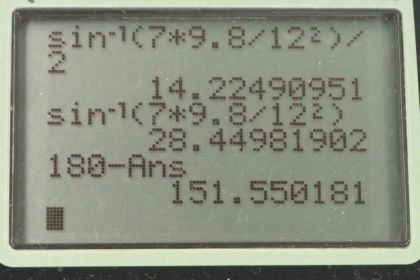
The equation used here is the range equation. It is not one of the regular kinematics equations. It contains gg with no negative sign in front. gg is always positive since it's a magnitude.

Hope this helps,
Shaun

Hello Sean,

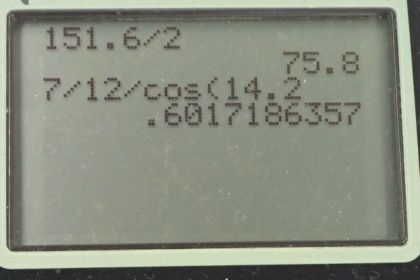
Thank you for your ongoing help. I have one question... at the end of this problem we divide x by Vox. (7/vox) with Vox being 12sin(14.2) to which I get 2.9437. Therefore, I plugged this in and took 7/2.9437 = 2.37797. I am unsure why you got 0.60s. I see on the image from your calculator that you did 12/cos(14.2)... can you explain why please?

No worries at all. Sometimes stepping away from a problem, then returning to it later, is the best problem solving tip if you've been working at problems for a while. The brain sometimes needs a rest, and it's always churning away at finding solutions even when you're doing other things like going for a walk.

I have a question regarding the inverse sin function. I have tried many different ways to type the equation into my calculator, but I am unable to get 14.2 degrees. When I hit the inverse sin function and put in (68.6/12) it keeps giving domain error. Is there a way to set up the equation to avoid this? Thanks.

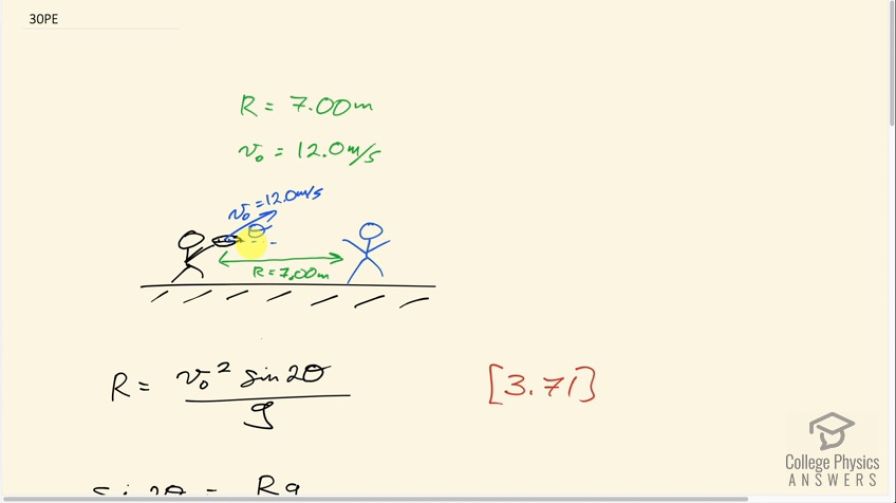
I am confused why in part C the equation used needs the initial velocity of X. Wouldn't using the equation x= initial position of x + ( initial velocity multiplied by time) + (1/2 multiplied by acceleration multiplied by time squared) also work?

Hi william, thank you for your question. If I understand your question correctly, you're wondering why in the solution I use the x-component of the initial velocity, vs your suggestion to use the initial velocity of 12.0 m/s given in the problem statement? The equation x=xi+vixt+12axt2x = x_\textrm{i} + v_{\textrm{i}x}t + \dfrac{1}{2}a_\textrm{x}t^2 applies only to one dimension, or in other words - to one axis. Every part of the equation needs to be concerned only with the components in that dimension, which in this case is the x-direction. We need the x-component of the initial velocity since the equation concerns only the x-direction.

I hope that helps,
Shaun